約数の意味と求め方を理解している。 6 公約数、最大公約数の意味と求め方を理解する。 整数を約数の観点から分類して考えている。 公約数、最大公約数の意味を理解している。 7 最大公約数を活用する具体的な場面を考え、公約数あるいは最大公約数についての理解を深める。 最大公約8月 27, 21 小学6年生 算数の練習問題プリントです。栄光ゼミナールの約7万名の生徒が自宅や教室で毎日挑戦している問題データベースから、定番の問題を集めて公開してい(1)ア~オ 整数の意味と表し方 (1)ア~オ 整数の意味と表し方 (100までの数など) (100までの数など) カ 簡単な3位数 キ 数を十を単位としてみること (2)ア・イ 整数の加法・減法 (2)ア・イ 整数の加法・減法 (1位数,加法・減法の場面を式に表す) (1位数)
Http Www Matsudo Ed Jp Html Matuga E Pdf
ひのあたいの求め方 整数
ひのあたいの求め方 整数-図形と方程式 図形と方程式 接線の式 数学2 円の方程式と 不定方程式の一つの整数解の求め方 数学系統 方程式は, 大概未知数の個数に対して式が同じ個数分用意されているもの でした. 例えば x 2 5x 6 = 0 は,未知数は x で 1 つ . 式は 1 つ です. 一方 不定 方程式 は, 未知数の個数に対して式がその




比の計算はこれで完璧 比の値の求め方と考え方
場合の数と確率~解き方のコツ・公式の問題など~ 2つの円の位置関係や、共通する接線の求め方など"図形と方程式での円"で頻出の問題をまとめて解説しました。基礎編、続編とともにご覧ください。 Shu Yasuda;理解を深めるとともに,整数の見方や数についての感覚を豊かにする」ことである。 本単元では,いくつかの集合に分類できる整数について,偶数,奇数,倍数,公倍数,最小公 倍数,約数,公約数,最大公約数といった観点から考察し,整数についての理解を深めていく。 特に,公倍数や最 求められる数(例:1.2、3 ・・・) ・0(ゼロ)から1ずつマイナスして 求められる数(例:-1、-2、-3 ・・・) のことです。 314などの少数や 2/3(3分の2)などの分数は もちろん整数ではありません。 言葉だと分かりにくいので 図で覚えてしまいましょう。 「自然数」とは つづ
3で割り切れる整数です。 C 3で割ると余りが0の整数です。 C 1・4・7は3で割ると余りが1の整数の仲間です。 C 2・5・8は3で割ると余りが2の整数の仲間です。 まず√3だけで考えると√3に一番近く、整数になるものは√1と√4だと分かります。√1=1 √4=2 つまり√1<√3<√4。 これを整数に直すと1<√3<2 11<√31<21 =2<√31<3 ここまで出来たらあとは簡単です。もっと簡単な見つけ方は、12の約数の中から、18の約数をみつける方法です。 12の約数→1 2 3 4 6 12 2つの数のうち小さい方の約数から、もう片方の数の約数にもなっているものを見つけます。 ③最大公約数の意味と見つけ方
1組の整数解を求めるときに,例えば,8 x +3 y =2 なら, すぐに, x =1, y =−2 とわかります。 このように,簡単な数値を代入してみてすぐにわかるときはよいのですが,すぐにわからなければこの問題のように,互除法を利用します。 それでは,これで回答を終わります。 これからも『進研ゼミ高校講座』にしっかりと取り組んでいってくださいね。 そのAx + by = c ( c ≠0)の整数解の表し方は何通りもあります。 自分の答えが正しいかどうか判断するには,求めた解に具体的な値を代入して, x と y の整数解が解答と同じになるかどうかを見ます。 例えば,3 x −7 y =1において,この整数解の1つとして原始根求め方, Cryptographic Mathematics 1 原始根の求め方 c = φ(m) とし,q 1, q 2,・・・, q k を数 c の互いに異なる素な約数とする.m と互いに素な数 g が法 m に関する原始根であるためには,この数 g が合同式 g (c/q 1) ≡ 1 (mod m), g (c/q 2) ≡ 1 (mod m),・・・, g 原始根の求め方ですが、一つの方法として




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




比を簡単にする Youtube
また,3x−7y=1の整数解の表し方は,x=7k−2,y=3k−1だけではなく最初の整数解の1つのとり方によって,何通りもあることも確認しておきましょう。 それでは,これからも『進研ゼミ高校講座』を活用して得点を伸ばしていきましょう! 数学のQ&Aランキング 数列Σの和の求め方 関数とオンライン整数列大辞典 以下のページは全て英語です。 この事典についての詳細は ようこそ をご覧ください。 Languages English Shqip العربية Bangla Български Català 中文 ( 正體字 , 简化字 (1) , 简 等式を満たす整数の組の求め方 Point:等式を満たす整数の組 解法の手順は、 ① 与えられた式を (式1) (式2)= (定数) の形に式変形します。 ② (定数)の約数より、 整数のかけ算で (定数)となる組合せ を書き並べます。 例えば、 のときは、 このとき




高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット
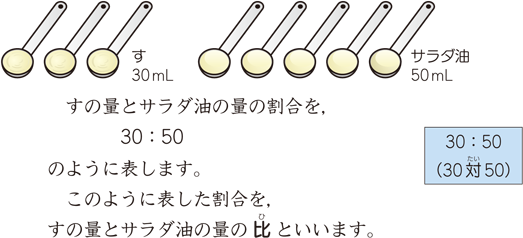



比と比の値 算数用語集
イ 乗数や除数が整数の場合の計 算の考え方を基にして、乗数や 除数が小数である場合の乗法及 び除法の意味について理解する こと。 ウ 小数の乗法及び除数の計算の 仕方を考え、それらの計算がで きること。また、あまりの大き さについて理解すること。 小数の乗法 分数の乗法及び除 法1次不定方程式の解を求めます。 けれど、手で計算するのも練習です。 検算などに使ってください。 0 以外の整数を入力してください。 負の数も入力できます。 数字とマイナス以外は無視されます。 x y = innerHTML innerText textContent 式番号の開始値 (A 25 ひのあたいの求め方 分数 ひのあたいの求め方 分数 リンクを取得 ;



Http Support Education Ne Jp Ela Katsuyou Ela Osusume S6 1g Pdf




6年算数 比 比の意味 比の値の求め方について 一緒に考えていきましょう Youtube
X=7k (kは整数) と表されます。これをもとの方程式に代入すると, 3・7k=7Y より,Y=3k となり,(☆)の整数解は, (X,Y)=(7k,3k) (kは整数) と求められます。 ≪方程式 3x−7y=1 の場合≫ それでは, 3x−7y=1 ・・・・・・(ア)A, b, c が整数であるとき, 1次方程式 axby=c (1) を満たす整数 x, y を求めよ という形の問題を扱う.(不定方程式の整数解とも呼ばれる.) 中学校以来習ってきたように (1)の形の方程式は xy 平面上の直線を表しており,その直線上の点 (x, y) はすべて方程式 (1)の解となっているから,解は無限にある.すなわち不定解になる. この頁では, x, y は整数という条件 ベストアンサー a:bの比の値はa/b=a÷b となって、 前の数値を後ろの数値で割れば出ますね。 分数の場合も同じで、(1/6)÷(1/9) =(1/6)×(9/1)=9/6=3/2・・・答え 分数の計算が嫌なら、比は両方に同じ数を掛けても 等号は成り立つので、たとえば、分母の最小公倍数の18を掛けると (1/6):(1/9)=(18/6):(18/9)=3:2 よって比の



十の位 一の位を入れかえてできる数 苦手な数学を簡単に
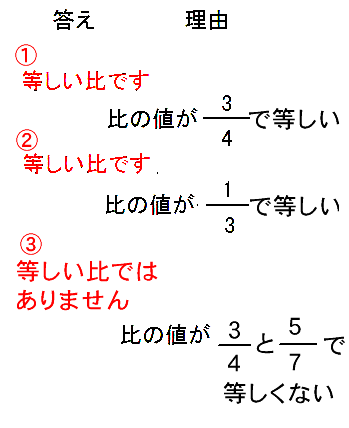



6年算数比とその利用2等しい比の教え方
次の にあてはまる数を求めなさい。 (1) 5=1× =5× 。 (2) 8=1× =2× =4× =8× 。 (3) 15=1× =3× =5× =15× 。 (4) 16=1× =2× =4× =8× =16× 。 (5) 24=1× =2× =3× =4× =6× =8× =12× =24× 。 (6) 36=1× =2× =3× =4× =6× =9× =12× =18× =36× 。分数×整数の計算の仕方を説明しましょう。(5年) わり算のきまりや分数×整数の計算の仕方を説明しよう。(5年) ②円周の長さの求め方を覚えていま すか。 2へ う ろ 返 り ふ 1へ う ろ 返 り ふ 円の面積=半径×半径×314 で求められます。 これまでに習った方法で円の面積を求め方をピタゴラス数とは ピタゴラス数とは,直角三角形の3辺の長さとなるような3つの整数の組のことです。 ピタゴラスの定理(三平方の定理)を使うと, a 2 b 2 = c 2 a^2b^2=c^2 a2 b2 = c2 を満たす自然数の組 ( a, b, c) (a,b,c) (a,b,c) をピタゴラス数と呼ぶ。 と




6年生算数ドリル 比と比の値




小6 算数 比と比の値 解説 動画 Youtube
整数部分+小数部分=√13 なので 小数部分=√13-整数部分 つまり、小数部分=√13-3 ――――――――――――――――――― でした^^: 雛 約1年前 ご丁寧にありがとうございます! この回答にコメントする 回答するにはログインが必要です。ROUND関数は、引数の「数値」を「桁数」まで表示するように四捨五入します。 引数の桁数は次のような関係になっています。 一の位を「0」と考えると、桁数0は、「小数点以下第一位を四捨五入して整数で表示する」ことになります。 また、小数点以下を表示させたい場合は、桁数「1」を指定すると小数点以下第二位を四捨五入します。 関数を入力するときは 固定小数点と浮動小数点の求め方について備忘録代わりに簡単に書いておく。 詳しい内容が知りたい場合は適宜調べてください。 固定小数点 固定小数点は整数型を小数として扱う事が出来る;



Www Pref Saitama Lg Jp Documents Shidouan Shou Sannsu Pdf




小6 算数 小6 15 比と比の値 Youtube
4/√51の整数部分と小数部分の求め方。教科書の解説。東京書籍 高校数学Ⅰ1章 数と式2節 実数問題
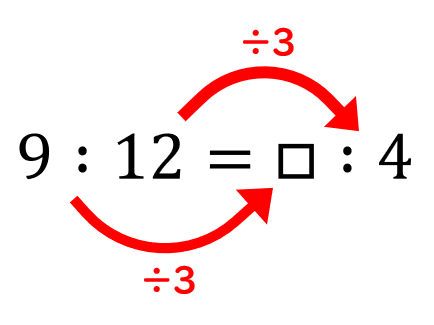



比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun



Http Www Torikyo Ed Jp Kyoiku C H29ad 04 3 Pdf




超簡単にわかる 中央値とは 苦手な数学を簡単に




比の計算問題 比を簡単にする方法は小学生でもできる 中学や高校の数学の計算問題



48s96ub7b0z5f Net Sankakuhi Sougo




比の値の求め方 小学生 中学生の勉強




比と比の値 その2 家庭学習レシピ
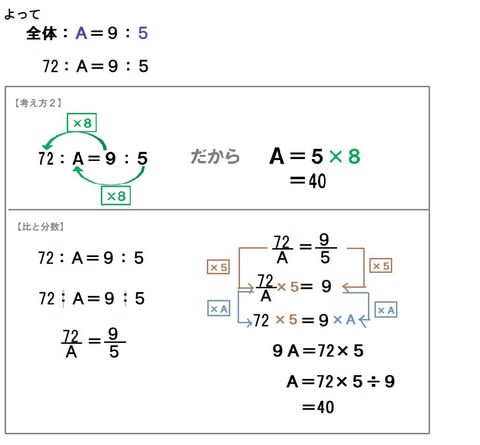



比の問題 小6 比と分数の関係 算数の教え方教えますmother S Math Happy Study Support



Http Www Kita9 Ed Jp Eductr Handbook Challengesheet Elementaryschool Sansuu 5 500 Pdf



6年算数比とその利用2等しい比の教え方



この比の値の求め方を教えて下さい A Bの比の値はa B A B Yahoo 知恵袋



Http Www Matsudo Ed Jp Html Matuga E Pdf




比の計算はこれで完璧 比の値の求め方と考え方




比と比の値についての自主学習ノート例 家庭学習レシピ



算数小6の問題です 分数の比を簡単にするという問題です 6 Yahoo 知恵袋




6年生算数ドリル 比と比の値



Http Menet Ed Jp Kaihigashi Es Information Action Common Download Main Upload Id 1753
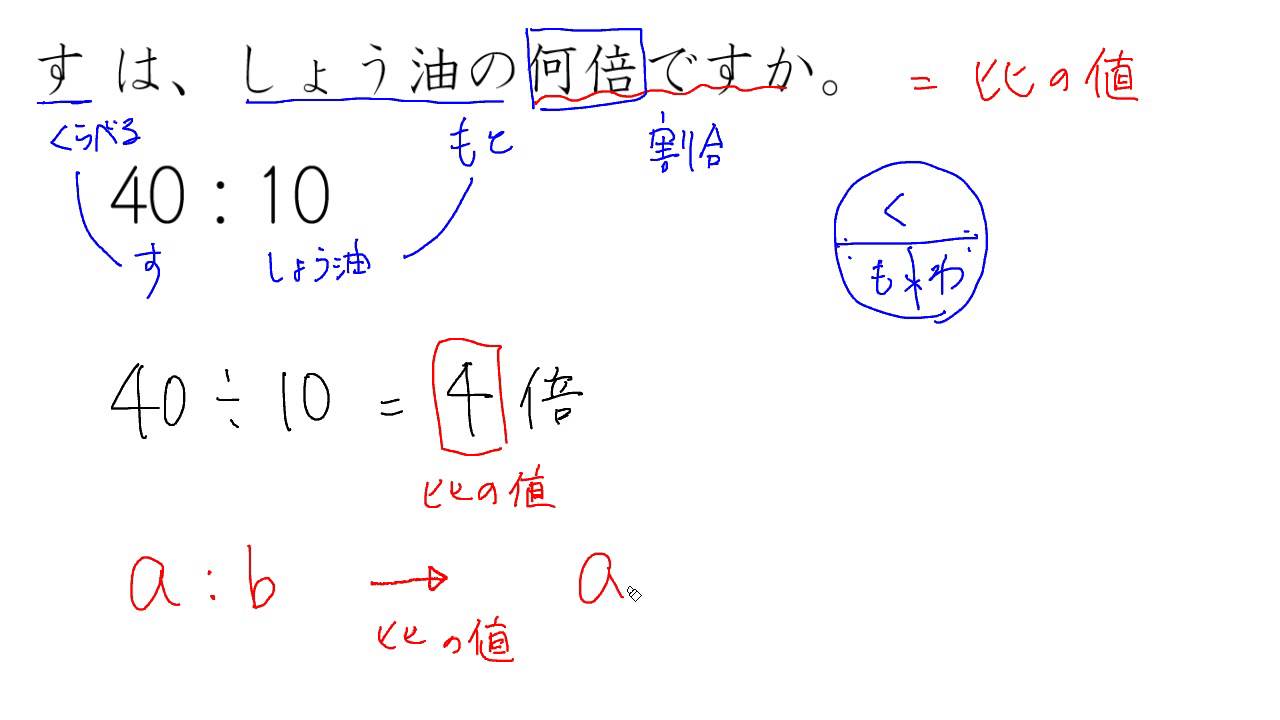



比の値 Youtube



比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun



Http Www Edu Tens Net Kyouikuken Basic Takamatsu Pdf Esan6 Answer S6 08ans Pdf



6年算数比とその利用2等しい比の教え方



Www Dainippon Tosho Co Jp Introduction21 Contents Files R3math Shuisho1 Pdf




比の計算はこれで完璧 比の値の求め方と考え方




6年生算数ドリル 比と比の値




6年生算数ドリル 比と比の値




6年生算数ドリル 比と比の値



6年算数比とその利用2等しい比の教え方
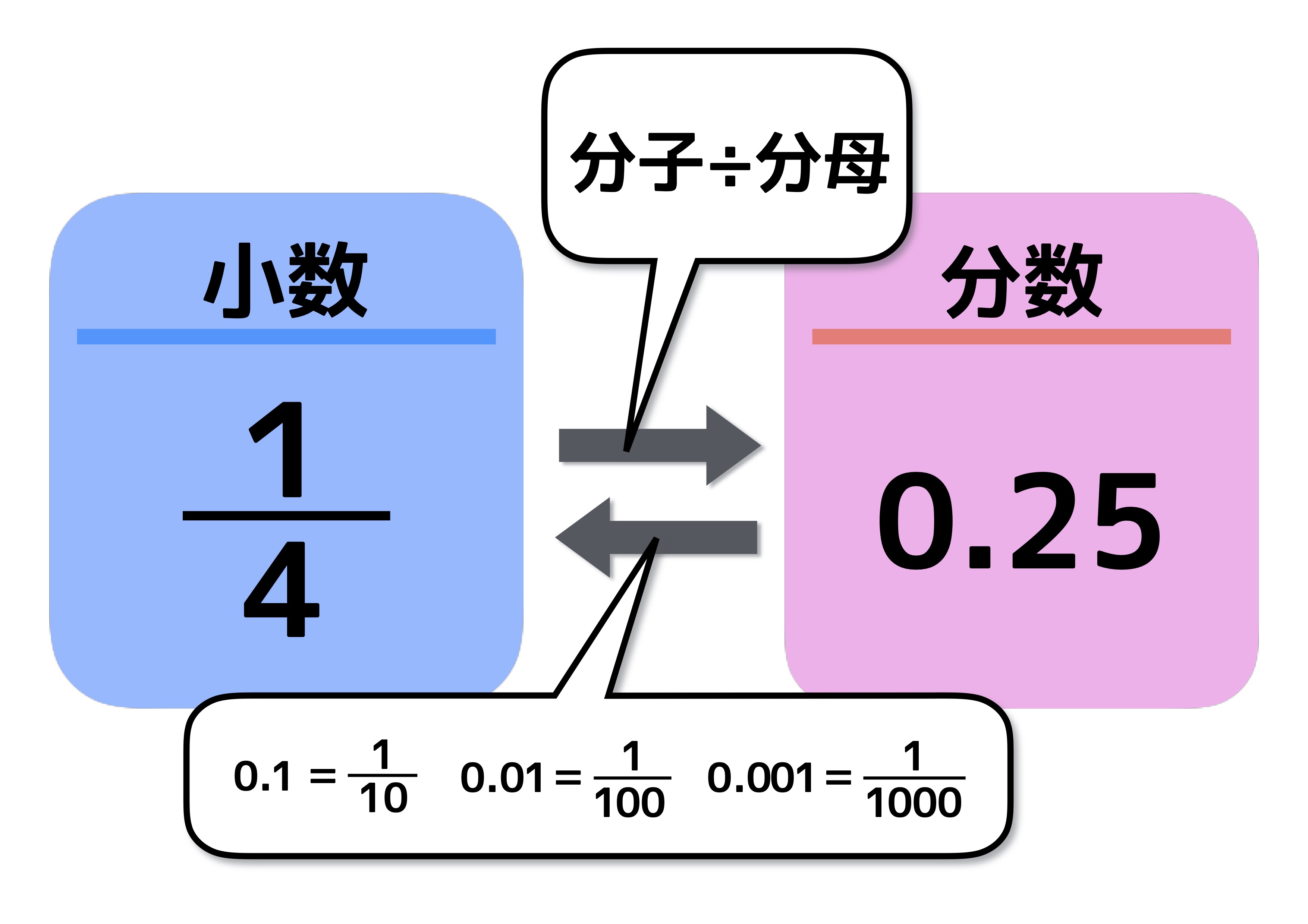



分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ



Http Www Torikyo Ed Jp Kyoiku C H29ad 04 3 Pdf




小6 算数 小6 16 比と比の値 Youtube



比の計算ドリル
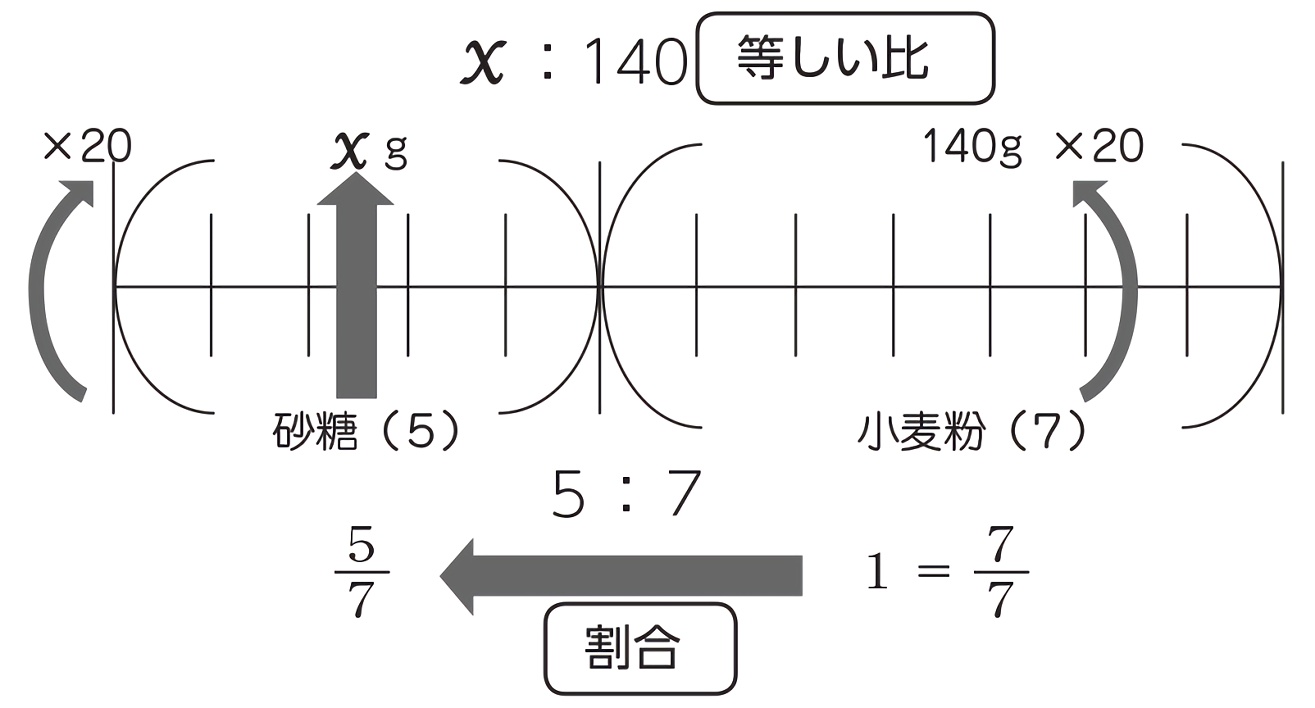



小6算数 比と比の値 指導アイデア みんなの教育技術




わかる 教えられる 小学校6年分の算数 高橋書店



3



比の値って 答えは分数なんですか 少数なんですか 整数のとき Yahoo 知恵袋




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




6年生算数ドリル 比と比の値




算数 比と比の値 小学生 算数のノート Clear




6年生算数ドリル 比と比の値




この2問が分からないので教えてください 人 Clear
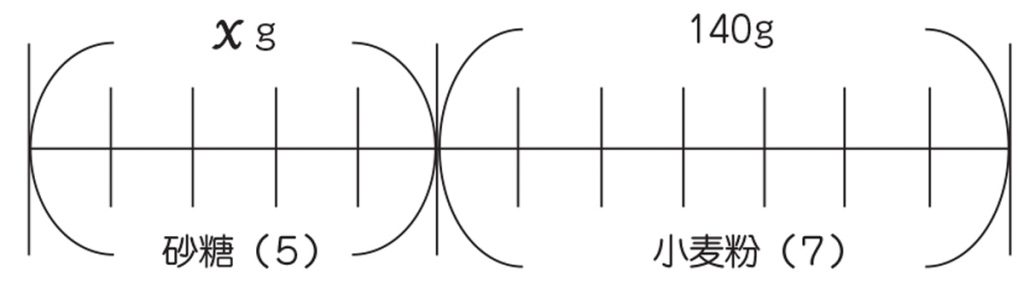



小6算数 比と比の値 指導アイデア みんなの教育技術



1




比例式の解き方とは 分数を用いた計算 かっこを含む文章問題をわかりやすく解説 遊ぶ数学




教えてください 今日の10時までにお願いします Clear
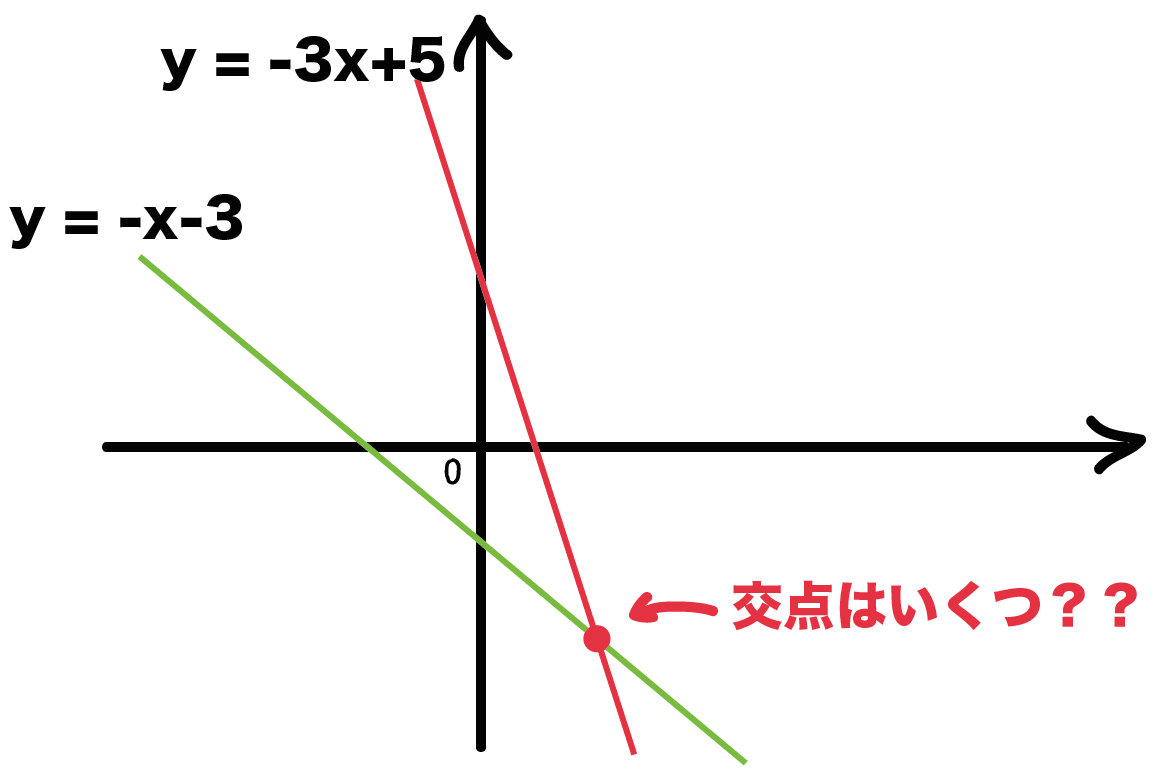



2直線の交点の座標の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




標準 三角関数の値 なかけんの数学ノート




この問題文の 3 がわかりません Clear



Cms Gakko Akiota Jp Kakesho Wysiwyg File Download 1 763



比の値の求め方 次の比の値の求め方を教えて下さい 0 4 0 25 比の Yahoo 知恵袋




整数nの値の求め方を 教えてください Clear




整数nの値の求め方を 教えてください Clear




最小値を求める問題をいろいろな方法で解いてみよう 高校数学 身勝手な主張




比の値 1 整数 6年生 比 まなび365 無料算数プリント



比例式とは 計算問題の解き方や利用問題 比例式の作り方 受験辞典



比の値って 答えは分数なんですか 少数なんですか 整数のとき Yahoo 知恵袋




比と比の値についての自主学習ノート例 家庭学習レシピ




比と比の値についての自主学習ノート例 家庭学習レシピ




数学 定期テストに出題される1次不等式を満たす整数の個数に関する問題 大学入試数学の考え方と解法



3
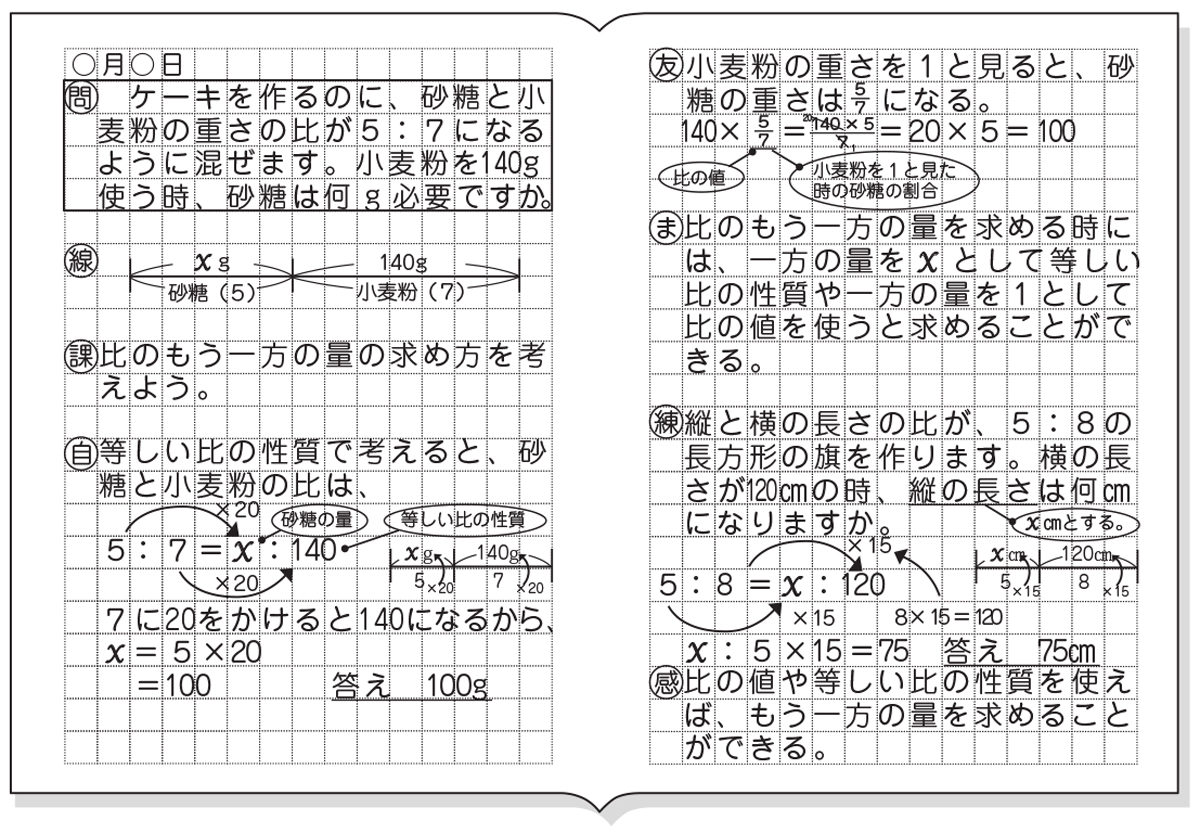



小6算数 比と比の値 指導アイデア みんなの教育技術
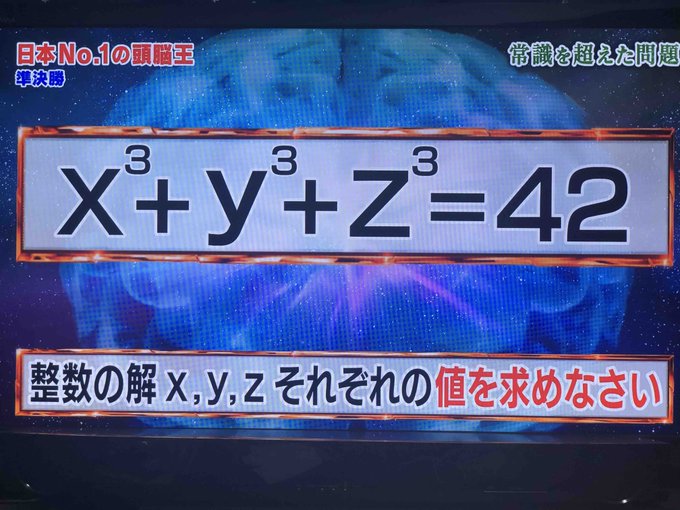



X 3 Y 3 Z 3 Kの整数解 頭脳王の問題から 理系のための備忘録




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




比の値 まなび365 小学生の算数プリントを自動作成 無料で自宅学習



Http Www Edu Tens Net Syohp Murehp Kyuukou Purinto Pridata 6nen 6san5 Pdf



Http Www Kochinet Ed Jp Ochi E Sidoan H30 62 Pdf




比とは何か を子どもに説明できますか 当社の顧客の男女比は7 3です President Online プレジデントオンライン




比の値 まなび365 小学生の算数プリントを自動作成 無料で自宅学習




比と比の値 身勝手な主張
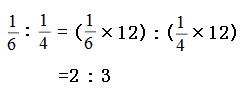



比の性質を解説 比例式や連比の解き方だってこんなに簡単



3



48s96ub7b0z5f Net Sankakuhi Sougo




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun
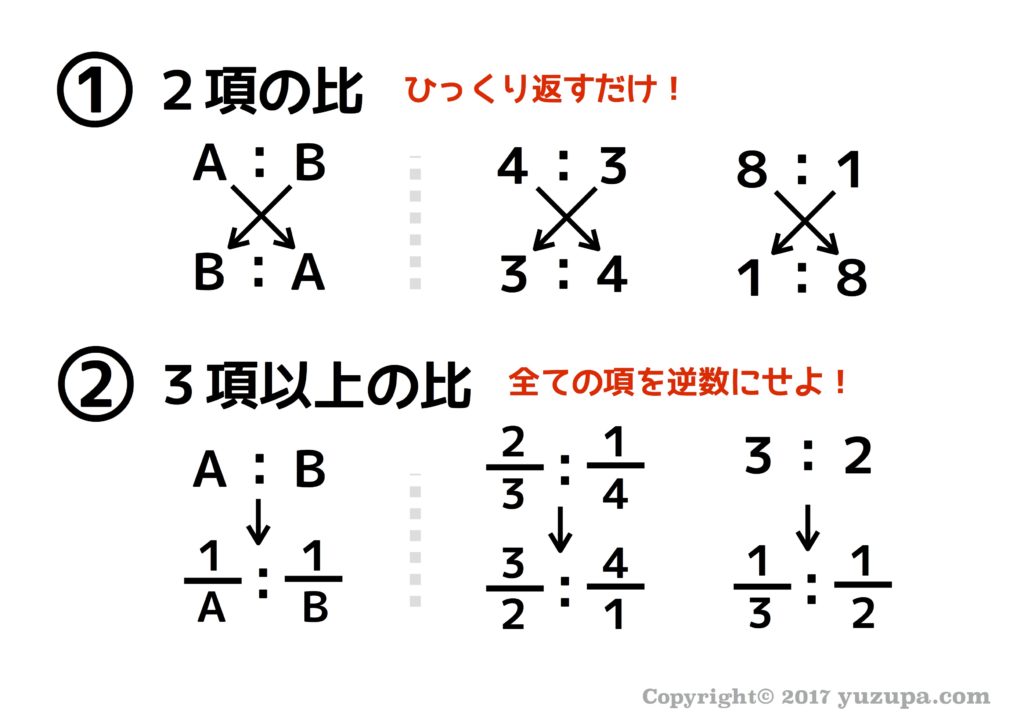



中学受験 割合と比は 7つ道具 で克服 かるび勉強部屋




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun
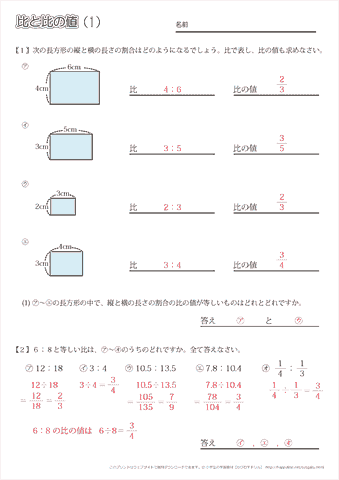



小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生



6年算数比とその利用2等しい比の教え方



2




比と比の値 その2 家庭学習レシピ
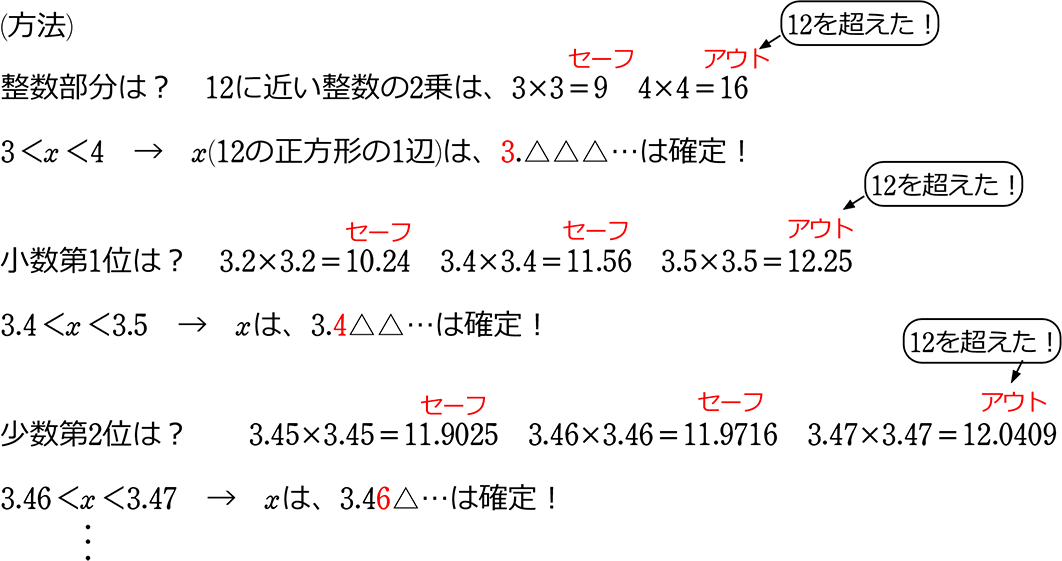



中学数学 平方根
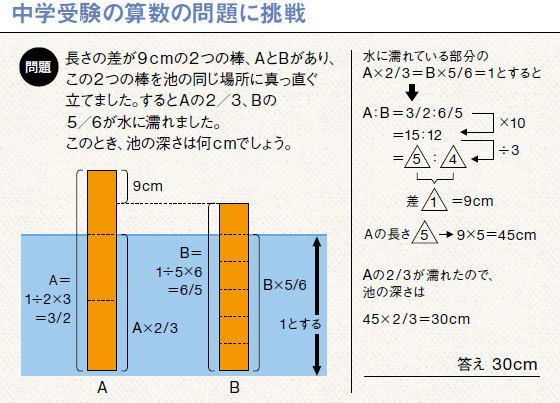



比とは何か を子どもに説明できますか 当社の顧客の男女比は7 3です President Online プレジデントオンライン




比の値 まなび365 小学生の算数プリントを自動作成 無料で自宅学習




比と比の値についての自主学習ノート例 家庭学習レシピ
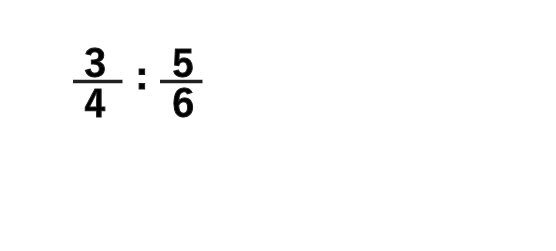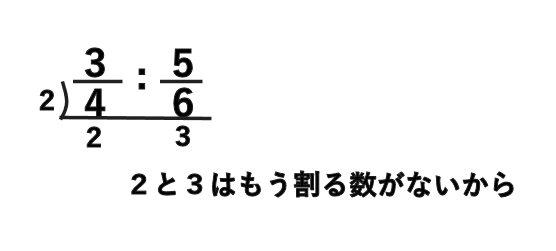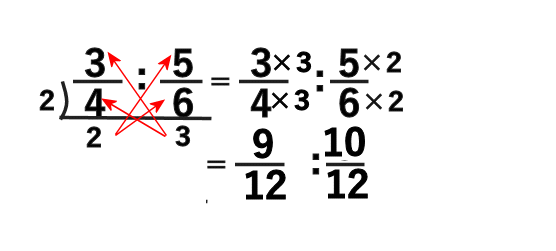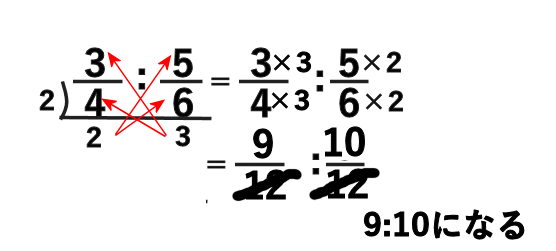



分数の比を簡単にする




比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun
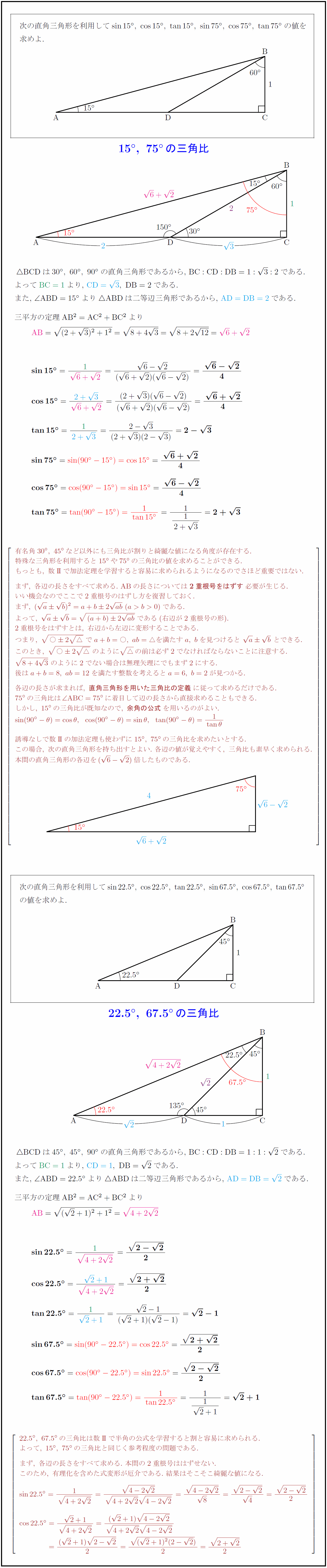



高校数学 15 75 22 5 67 5 の三角比の値の図形的な求め方 受験の月




小6 算数 小6 17 比と比の値 文章題 Youtube
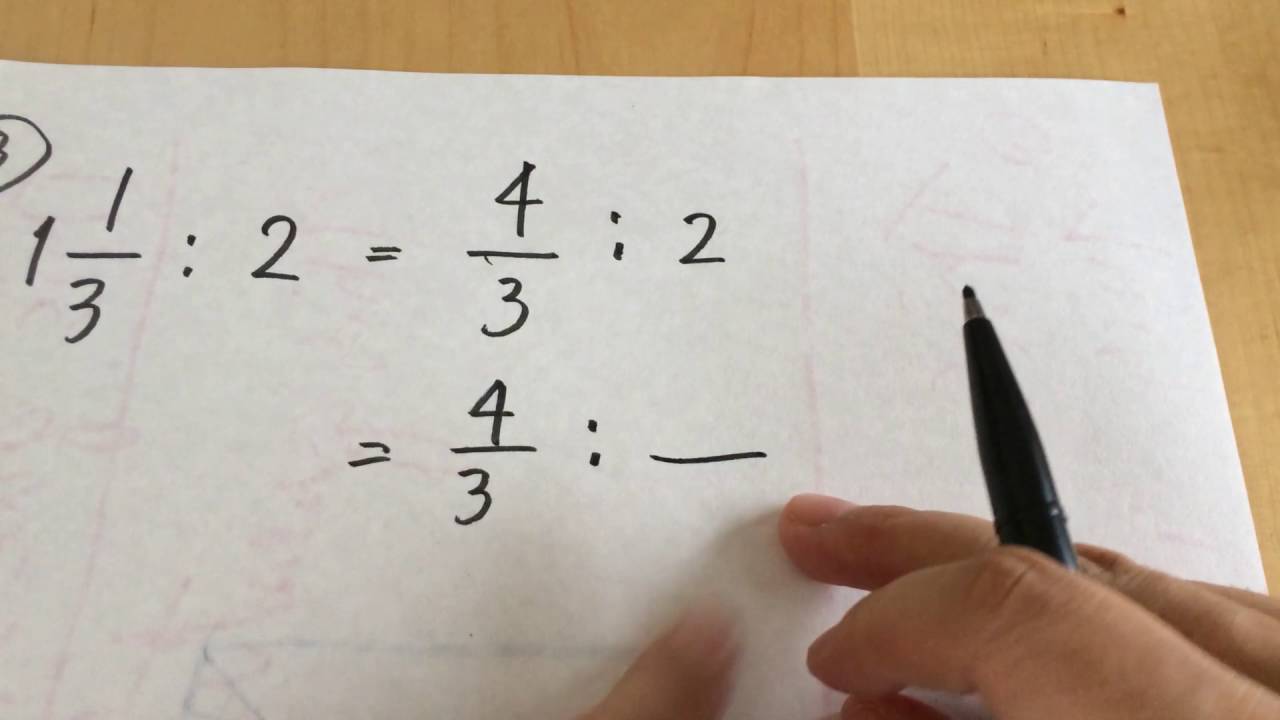



比を簡単にする Youtube



甘楽町立新屋小学校
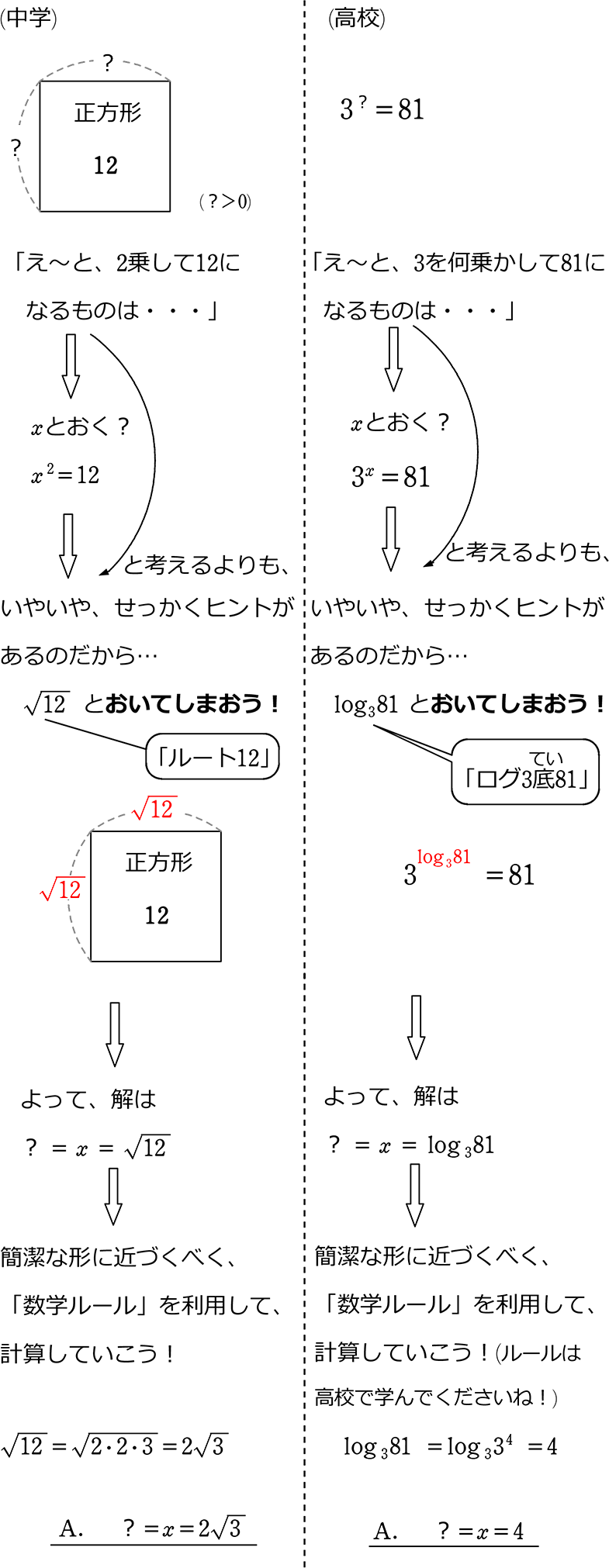



中学数学 平方根



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典



比の値って 答えは分数なんですか 少数なんですか 整数のとき Yahoo 知恵袋




比と比の値の論争をめぐって 私的な感想 身勝手な主張



0 件のコメント:
コメントを投稿